
特徴抽出による情報圧縮(主成分分析)|Pythonで機械学習vol.7
- Python
- 機械学習

ここで機械学習の種類についてご説明します。
一般的に機械学習は、大きく下の3種類に分けられます。
・教師あり学習
・教師なし学習
・強化学習
今回は教師あり学習に焦点をあてているため、その他の種類については説明しません。
興味がある方はGoogle先生に聞いてみてください。
教師あり学習とは、簡潔に言うと「データと正解(またはラベル)のペアを与えて、それをもとに学習する方法」です。
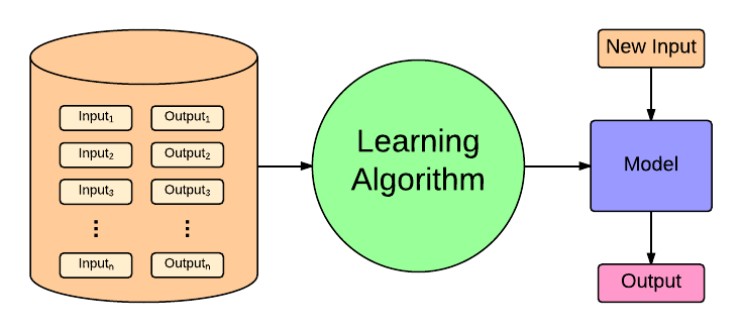
上の図がわかりやすいかと思うのですが、答え(ラベル)を持ったデータセットを用いて入力と出力を繰り返すことでモデルを構築し、全く新しいデータが入力された際にそのモデルが答えを予測して出力します。
この与えられるデータセットを訓練データや学習データといいます。
今回はscikit-learnで用意されているサンプルデータセットを使い、Numpyの関数を使いながら線形回帰について学んでいきます。
Pythonのオープンソース機械学習ライブラリのことで、以下のような特徴があります。
・NumPy, SciPy や Matplotlib と互換性を持つように開発されている。例えば、NumPyで作成した行列を機械学習の入力データとして扱うことができる。
・オープンソース (BSD ライセンス) で公開されており、無料で利用できるだけでなく、商用にも利用可能。
・クラスタリングや回帰、分類器、次元圧縮、データの前処理をはじめとする、機械学習のアルゴリズムを幅広く実装しています。
今回利用するデータセットはボストンの住宅価格です。
まずは前回説明した通りターミナル、もしくはコマンドプロンプトから任意のディレクトリでJupyterを起動します。
$ jupyter notebook
起動したら新規ファイルを作成して編集画面を表示します。
そして、今回利用する分析用ライブラリーを下のコマンドでインポートします。
(お忘れかもしれませんが、コマンドの実行は Shit+Enter です)
import numpy as np
import pandas as pd
from pandas import Series,DataFrame
また、データを可視化するために下のグラフ描画ライブラリーもインポートします。
import matplotlib.pyplot as plt
%matplotlib inline
そして、最後にデータを読み込むために、次のモジュールをインポートします。
from sklearn.datasets import load_boston
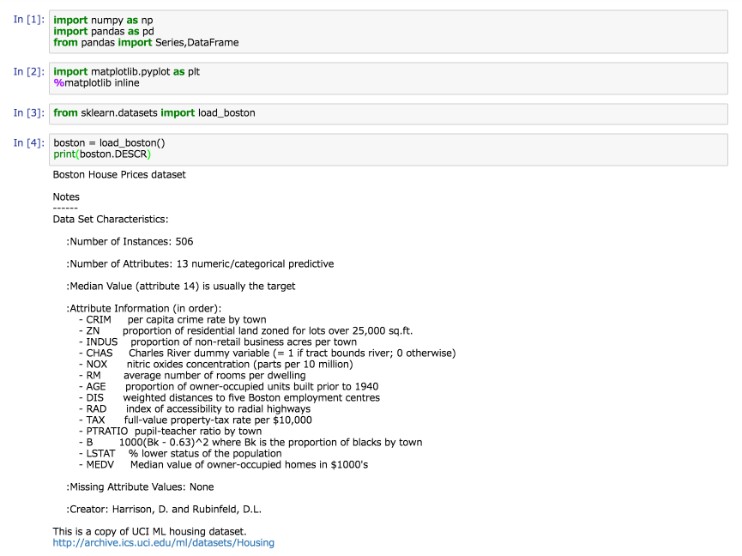
では、実際にサンプルデータを読み込んでデータ概要を表示してみましょう。
boston = load_boston()
print(boston.DESCR)
すると下のようにデータについての説明が英語で表示されます。
ここにはインスタンス数(データの数)や街の犯罪率、税率といった含まれているデータの特徴が記載されています。
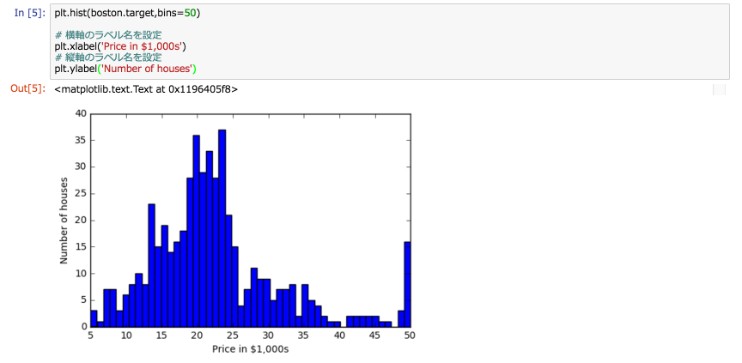
それではmatplotlibの関数をつかって、データをヒストグラム化して可視化してみましょう。
plt.hist(boston.target,bins=50)
# 横軸のラベル名を設定
plt.xlabel('Price in $1,000s')
# 縦軸のラベル名を設定
plt.ylabel('Number of houses')
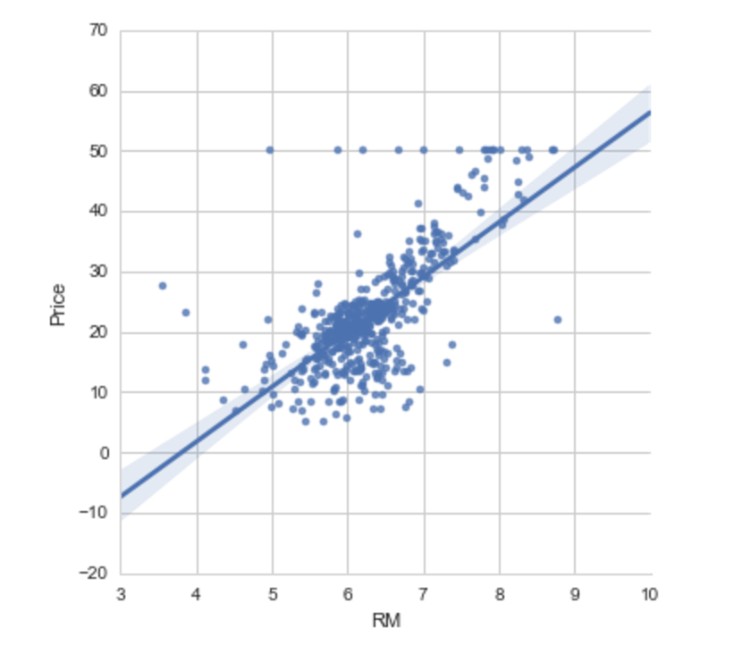
次に部屋の数と価格の関係を見るために散布図を描いてみます。
# ラベルがRMとなっている5番目の列が部屋数
plt.scatter(boston.data[:,5],boston.target)
plt.ylabel('Price in $1,000s')
plt.xlabel('Number of rooms')
実際に解いてみる前に簡単に線形回帰とはなにかについて理解しましょう。
色々調べてわかりやすい表現をさがしてみたのですが、線形回帰についてとても良くまとまっているものがあったのでそちらのリンクを張ります。
線形回帰(前編)http://gihyo.jp/dev/serial/01/machine-learning/0008
線形回帰(後編)http://gihyo.jp/dev/serial/01/machine-learning/0009
とっってもシンプルにいうと、下のように与えられたどのデータからも1番近い距離にあたるように線を引くということです。
そして、その線を引くことによって新しく入手したデータがどこに位置づけられるのかを予測することが出来ます。
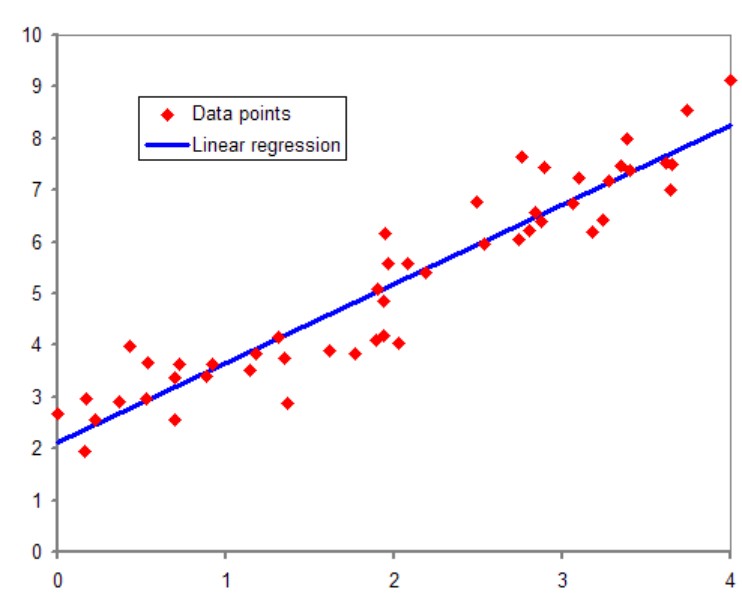
では実際に線形回帰を解いていきましょう。
まずは、データを使いやすいようにpandas.DataFrameを導入します。
# DataFrameを作成
boston_df = DataFrame(boston.data)
# 列名をつける
boston_df.columns = boston.feature_names
# 新しい列を作り目的変数である価格を格納
boston_df['Price'] = boston.target
boston_df.head()
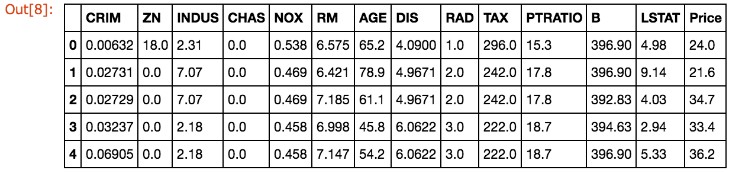
今回は説明変数が複数存在するので重回帰を考え、scikit-learnの線形回帰ライブラリを利用します。
sklearn.linear_model.LinearRegressionクラスは、データを元にモデルを作り、予測値を返すことができます。
モデルを作る時には、fit()メソッドを呼び、予測をするときは、predict()メソッドを使います。
今回は重回帰モデルを使いますが、他のモデルも同じように、fitとpredictメソッドを実装しているところが、scikit-learnの便利なところです。
まずは必要なライブラリーをインポートし、LinearRegressionクラスのインスタンスを作ります。
import sklearn
from sklearn.linear_model import LinearRegression
lreg = LinearRegression()
次にボストンの住宅価格を、目的変数としてX_multiに格納します。
# 説明変数
X_multi = boston_df.drop('Price',1)
通常、機械学習のプログラムを組む際には、一部のデータを使ってモデルを作り(Training)、残りのデータを使ってモデルを検証する(Validation)ということができます。
scikit-learnではこのサンプルデータの住み分けをよしなにやってくれる便利な関数 train_test_split があります。
# 説明変数をX、目的変数をYとして格納
X_train, X_test, Y_train, Y_test = sklearn.cross_validation.train_test_split(X_multi,boston_df.Price)
# 中身を確認
print(X_train.shape, X_test.shape, Y_train.shape, Y_test.shape)
次に学習用のデータを使ってモデルを作り、残りのデータを使って住宅価格を予測してみます。
※lreg.fit() はデータを元にモデルを作り、lreg.predict() は作られたモデルを元に予測値を返す。
# fit関数でモデル生成
lreg.fit(X_train,Y_train)
予測を学習用のデータと、テスト用のデータの両方で行うことで、それぞれの平均二乗誤差を計算できます。
pred_train = lreg.predict(X_train)
pred_test = lreg.predict(X_test)
print('X_trainを使ったモデルの平均二乗誤差={:0.2f}'.format(np.mean((Y_train - pred_train) ** 2)))
print('X_testを使ったモデルの平均二乗誤差={:0.2f}'.format(np.mean((Y_test - pred_test) ** 2)))
また回帰分析では、実際に観測された値と、モデルが予測した値の差を、残差と呼びます。
横軸に予測値、縦軸に実際の値との差をプロットしたものを残差プロットと呼びます。
残差プロットを描いて、多くのデータがy=0の直線に近いところに集まれば、よいモデルが出来たということになります。
# 学習用データの残差プロット
train = plt.scatter(pred_train,(pred_train-Y_train),c='b',alpha=0.5)
# テスト用データの残差プロット
test = plt.scatter(pred_test,(pred_test-Y_test),c='r',alpha=0.5)
# y=0の水平線
plt.hlines(y=0,xmin=-10,xmax=50)
plt.legend((train,test),('Training','Test'),loc='lower left')
plt.title('Residual Plots')
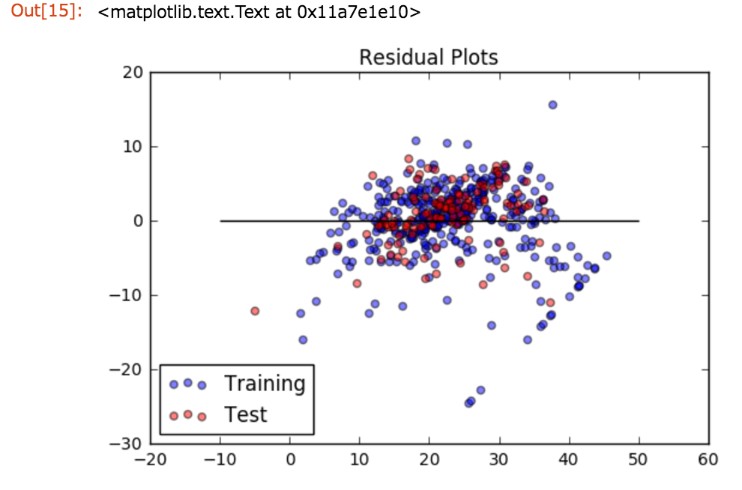
実行結果をみるとy=0の回りに、残差がランダムにばらけているように見えます。
つまり、未知のデータ(テストデータ)が入力された際に、実際の観測値とモデルが予測した値の差が小さい、つまり良い予測がされているということなので、このモデルは良かったと言えそうです。
今回は教師あり学習についての概要説明と、実際にボストンの不動産価格をサンプルに線形回帰問題を解くところまでを行いました。
利用したライブラリーについて詳しい説明は省きましたが、更に理解を深めたい場合は、下記のドキュメントなどに有用な情報が多くありますので是非チェックしてみてください。
▼scikit-learn
http://scikit-learn.org/stable/modules/linear_model.html
▼matplotlib
http://matplotlib.org/2.0.0/py-modindex.html
▼pandas.DataFrame
http://pandas.pydata.org/pandas-docs/stable/generated/pandas.DataFrame.html
次回はシリーズ第3弾として、分類問題を解く方法、ロジスティック回帰を使ってみます。
今後もお楽しみに!